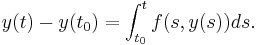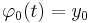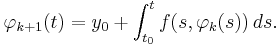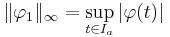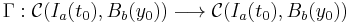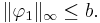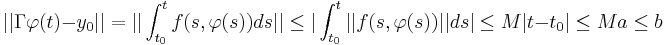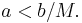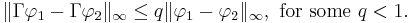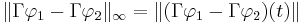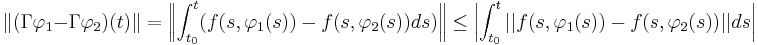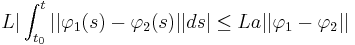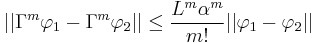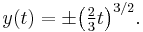Picard–Lindelöf theorem

Consider the initial value problem

$y'(t)=f(t,y(t)),\quad y(t_0)=y_0, \quad t \in [t_0-\varepsilon, t_0%2B\varepsilon].$

Suppose $f$ is Lipschitz continuous in $y$ and continuous in $t$ . Then, for some value 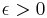$\epsilon>0$ , there exists a unique solution 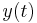$y(t)$ to the initial value problem within the range $[t_0-\epsilon, t_0%2B\epsilon]$ .^[1]

Proof sketch

The proof relies on transforming the differential equation, and applying fixed-point theory. By integrating both sides, any function satisfying the differential equation must also satisfy the integral equation

$y(t) - y(t_0) = \int_{t_0}^{t} f(s,y(s)) ds.$

A simple proof of existence of the solution is obtained by successive approximations. In this context, the method is known as Picard iteration.

Set

$\varphi_0(t)=y_0 \,\!$

and

$\varphi_{k%2B1}(t)=y_0%2B\int_{t_0}^{t}f(s,\varphi_k(s))\,ds.$

It can then be shown, by using the Banach fixed point theorem, that the sequence of "Picard iterates" 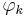$\varphi_k \,\!$ is convergent and that the limit is a solution to the problem. Exploiting the fact that the width of the interval where the local solution is defined is entirely determined by the Lipschitz constant of the function,one can assure global existence of the solution, i.e. the solution exists and is unique until it leaves the domain of definition of the ODE. An application of Grönwall's lemma to 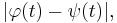$|\varphi(t)-\psi(t)|,$ where $\varphi$ and $\psi$ are two solutions, shows that $\varphi(t)=\psi(t)$ , thus proving the global uniqueness (the local uniqueness is a consequence of the uniqueness of the Banach fixed point).

Detailed proof

Let 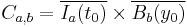$C_{a,b}=\overline{I_a(t_0)}\times\overline{B_b(y_0)}$ be the compact cylinder where $f$ is defined, this is

$t\in\overline{I_a(t_0)}=[t_0-a,t_0%2Ba]$ and $\overline{B_b(y_0)}=[y_0-b,y_0%2Bb]$ .

Let

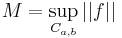$M=\displaystyle\sup_{C_{a,b}}||f||$ ,

this is, the maximum slope of the function in modulus. Finally, let $L$ be the Lipschitz constant of $f$ with respect to the second variable.

We will proceed to apply Banach fixed point theorem using the metric on 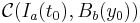$\mathcal{C}(I_{a}(t_0),B_b(y_0))$ induced by the uniform norm

$\| \varphi_1 \|_\infty = \sup_{t \in I_a} | \varphi(t)|$

We define an operator between two functional spaces of continuous functions, Picard's operator, as follows:

$\Gamma:\mathcal{C}(I_{a}(t_0),B_b(y_0))\longrightarrow \mathcal{C}(I_{a}(t_0),B_b(y_0))$

defined by:

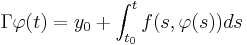$\Gamma \varphi(t) = y_0 %2B \displaystyle\int_{t_0}^{t} f(s,\varphi(s))ds$ .

We impose that it is well-defined, in other words, that its image must be a function taking values on 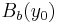$B_b(y_0)$ , or equivalently, that the norm of

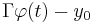$\Gamma\varphi(t)-y_0$ is less than $b$ ,

which can be restated as

$\| \varphi_1 \|_\infty \le b.$

$||\Gamma\varphi(t)-y_0||=||\displaystyle\int_{t_0}^{t} f(s,\varphi(s))ds||\leq |\displaystyle\int_{t_0}^{t} ||f(s,\varphi(s))||ds|\leq M|t-t_0|\leq M a\leq b$

The last step is the imposition, so we are impose the requirement

$a<b/M.$

Let us impose now the Picard's operator to be contractive under certain hypothesis over $a$ that later on we will be able to omit.

Given two functions 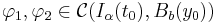$\varphi_1,\varphi_2\in\mathcal{C}(I_{\alpha}(t_0),B_b(y_0))$ , in order to appy the Banach fixed point theorem we want

$\| \Gamma \varphi_1 - \Gamma \varphi_2 \|_\infty \le q \| \varphi_1 - \varphi_2 \|_\infty, \text{ for some } q < 1.$

So let $t$ be such that

$\| \Gamma \varphi_1 - \Gamma \varphi_2 \|_\infty = \|(\Gamma\varphi_1 - \Gamma\varphi_2)(t)\|$

then using the definition of $\Gamma$

$\|(\Gamma\varphi_1 - \Gamma\varphi_2)(t)\| = \left \|\displaystyle\int_{t_0}^{t}(f(s,\varphi_1(s))-f(s,\varphi_2(s))ds)\right \|\leq \left | \displaystyle\int_{t_0}^{t}||f(s,\varphi_1(s))-f(s,\varphi_2(s))||ds \right |$

Then since $f$ is Lipschitz with respect to the second variable, we have that:

$L|\displaystyle\int_{t_0}^{t}||\varphi_1(s)-\varphi_2(s)||ds| \leq L a ||\varphi_1-\varphi_2||$

This is contractive if 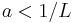$a <1/L$ .

We have established that the Picard's operator is a contraction on the Banach spaces with the metric induced by the uniform norm. This allows us to apply the Banach fixed point theorem to conclude that the operator has a unique fixed point. In particular, there is a unique function

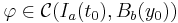$\varphi\in \mathcal{C}(I_{a}(t_0),B_b(y_0))$ such that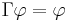 $\Gamma\varphi=\varphi$

This function is the unique solution of the initial value problem, valid on the interval 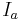$I_a$ where $a$ satisfies the condition

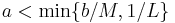$a < \min\{ b/M,1/L\}$ .

Optimization of the solution's interval

Nevertheless, there is a corollary of the Banach fixed point theorem that states that if an operator 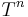$T^n$ is contractive for some 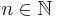$n\in\mathbb{N}$ then $T$ has a unique fixed point. We will try to apply this theorem to the Picard's operator. But before doing that, let us recall a lemma that will be very useful to apply the aforementioned corollary.

Lemma:

$||\Gamma^m \varphi_1 - \Gamma^m\varphi_2|| \leq \frac{L^m\alpha^m}{m!}||\varphi_1-\varphi_2||$

We will check this by induction:

For 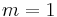$m=1$ we have already seen it, let us suppose it is true for 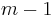$m-1$ and let us check it for $m$ :

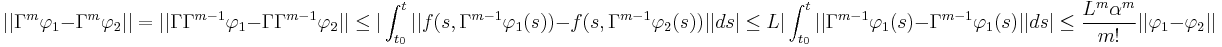$||\Gamma^m \varphi_1 - \Gamma^m\varphi_2|| =||\Gamma\Gamma^{m-1} \varphi_1 - \Gamma\Gamma^{m-1}\varphi_2|| \leq |\displaystyle\int_{t_0}^{t}||f(s,\Gamma^{m-1}\varphi_1(s))-f(s,\Gamma^{m-1}\varphi_2(s))||ds |\leq L|\displaystyle\int_{t_0}^{t}||\Gamma^{m-1}\varphi_1(s)-\Gamma^{m-1}\varphi_1(s)||ds|\leq \frac{L^m\alpha^m}{m!}||\varphi_1 - \varphi_2||$ .

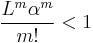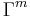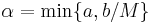Therefore, taking into account this inequality we can assure that for some $m$ large enough, the quantity $\frac{L^m\alpha^m}{m!}<1$ and hence $\Gamma^m$ will be contractive. So by the previous corollary $\Gamma$ will have a unique fixed point. So, finally, we have been able to optimize the interval of the solution by taking $\alpha=\min\{a,b/M\}$ .

The importance of this result is that the interval of definition of the solution does eventually not depend on the Lipschitz constant of the field, but essentially depends on the interval of definition of the field and its maximum absolute value of it.

Other existence theorems

The Picard–Lindelöf theorem shows that the solution exists and that it is unique. The Peano existence theorem shows only existence, not uniqueness, but it assumes only that ƒ is continuous in y, instead of Lipschitz continuous. For example, the right-hand side of the equation y ′ = y^1/3 with initial condition y(0) = 0 is continuous but not Lipschitz continuous. Indeed, the solution of this equation is not unique; two different solutions are given besides the trivial one 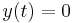$y(t) = 0$

$y(t) = \pm\big(\tfrac23t\big)^{3/2}.$ ^[2]

Even more general is Carathéodory's existence theorem, which proves existence (in a more general sense) under weaker conditions on ƒ.

Notes

^ Coddington & Levinson (1955), Theorem I.3.1
^ Coddington & Levinson (1955), page 7

References

Coddington, Earl A.; Levinson, Norman (1955), Theory of Ordinary Differential Equations, New York: McGraw-Hill .
E. Lindelöf, Sur l'application de la méthode des approximations successives aux équations différentielles ordinaires du premier ordre; Comptes rendus hebdomadaires des séances de l'Académie des sciences. Vol. 114, 1894, pp. 454–457. Digitized version online via http://gallica.bnf.fr/ark:/12148/bpt6k3074r/f454.table . (In that article Lindelöf discusses a generalization of an earlier approach by Picard.)

Picard–Lindelöf theorem

Contents